This is an old revision of the document!
XAS
Example three calculates the $2p$ to $3d$ x-ray absorption spectra of transition metal compounds in cubic symmetry. It does so on a crystal field theory level. (Not the most accurate, but very informative. Ligand field calculations can be found later in the tutorials) As input it requires the ion name, the scaling factor for the Slater integrals, the size of the crystal field, a possible magnetic field and a temperature. The output contains the x-ray absorption spectra for all possible polarizations. Besides plots of a few standard polarizations the conductivity tensor is given, which allows one to create any experimental geometry possible.
This is a nice little script to play with and learn what x-ray absorption spectroscopy measures. For example have a look how the linear and circular dichroism change in NiO (Ni$^{2+}$ with 10Dq=1.1, red=0.9 or so) as a function of temperature. You can see these in the conductivity tensor.
The configuration file is:
- conf.in
-- 3d ion (e.g. Sc ... Cu) : ion = "Ni" -- Universal scaling parameter for the Slater integrals (beta): beta = 0.90 -- Cubic Crystal Field Strength (10Dq) [eV] tenDq = 1.1 -- External magnetic field Bext [Tesla] Bx = 5 ; By = 0 ; Bz = 10 -- Temperature [Kelvin] T = 1
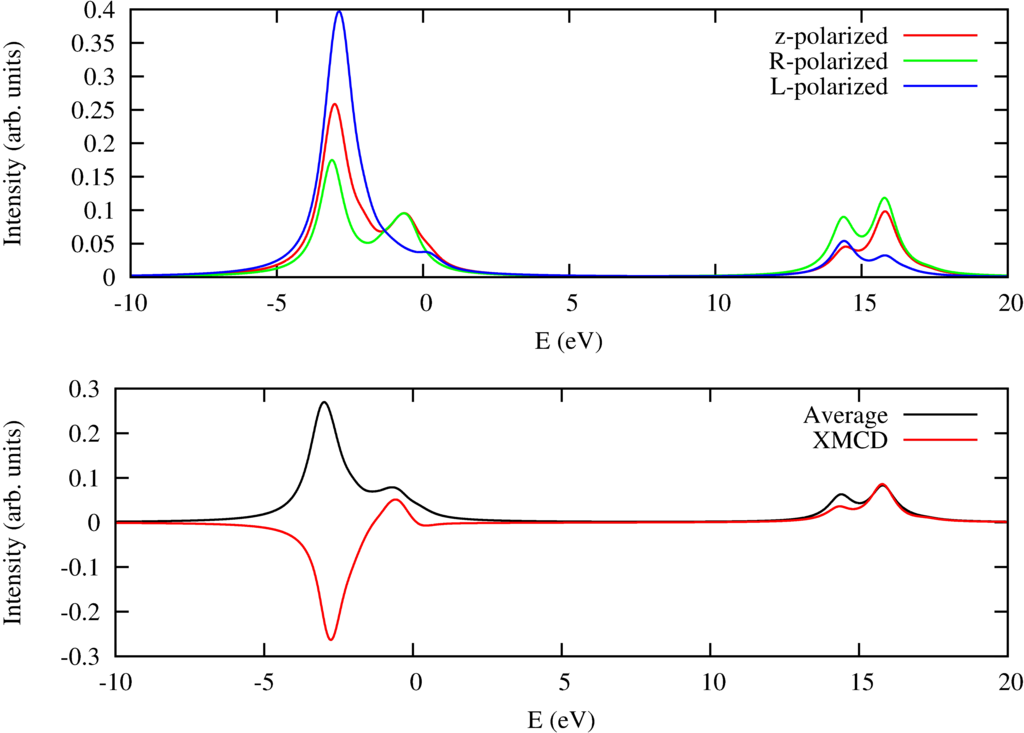
$L_{2,3}$ x-ray absorption spectra of Ni$^{2+}$ including magnetic circular dichroism.
Besides some text this program also creates plots of the x-ray absorption spectra. In the configuration file the magnetic field is set in the $(102)$ direction. The temperature is $1$ Kelvin and as the field size in the $z$ direction is 10 Tesla the Ni ion will be fully magnetically polarized. One can calculate the magnetic circular dichroic spectra by calculating the spectra for left and right circular polarized light and calculating the difference. This is done in this example and in the figure above one can see in the top pannel the XAS for $z$, $R$ (right circular) and $L$ (left circular) polarized light. The bottom pannel shows the isotropic spectra and the magnetic circular dichroic spectrum.
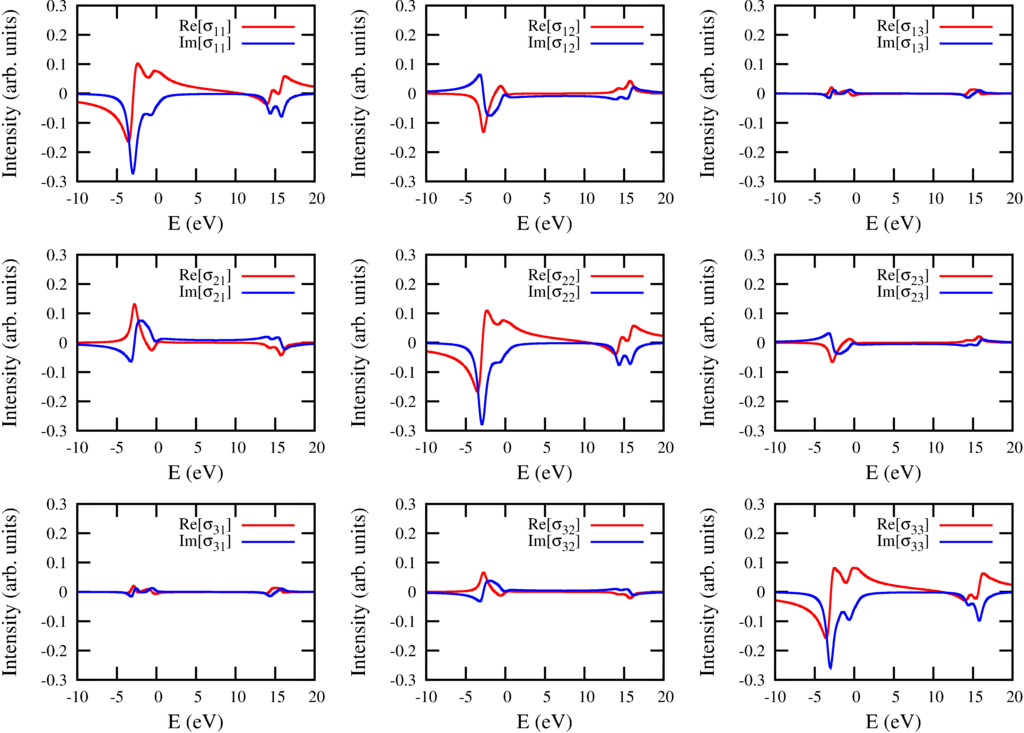
The conductivity tensor for excitations from $2p$ to $3d$ in Ni$^{2+}$
In principle one can calculate the spectra for any magnetic field direction, but also for any polarization direction. The Poyinting vector must not be in the $z$ direction and there are thus infinite possibilities to define left circular polarized light. In optics this is solved by calculating the optical conductivity tensor. This is a three by three matrix that describes the optical properties of the material for any posible polarization. If $\sigma(\omega)$ is the energy dependent conductivity tensor (three by three matrix) and $\varepsilon$ the polarization (a vector of length three) then the absorption is give as: $I_{XAS} = -\mathrm{Im}[\varepsilon^* \cdot \sigma(\omega) \cdot \varepsilon$. The conductivity tensor for Ni$^{2+}$ with a field in the $(102)$ direction is shown in the figure above.
The figure above shows several interesting features. The diagonal elements show magnetic linear dichroism, but also some of the off diagonal elements are influenced by magnetic linear dichroism. The $yz$ component for example is symmetric (equal to the $zy$ component) and also given by a magnetic linear dichroic effect. (See Phys. Rev. B 82 094402 (2010)). The magnetic circular dichroism due to the field in the $z$ direction can be found as the antisymmetric part of $xy$ and $yx$. The magnetic circular dichroism due to the field in the $x$ direction can be found as the antisymmetric part of $yz$ and $zy$.
Information on the ground state is given in the text output, which is:
- XAS.out
--> This program is the spectra calculator. --> Assuming a specific ionic configuration for Me^{2+} , the L-edge spectra are produced and plotted in a separate file. --> Chosen parameters are as follows: Ion beta 10Dq Bext(x) Bext(y) Bext(z) Temperature Ni 0.9000000 1.1000000 5.0000000 0.0000000 10.0000000 1.00 ---> Setting up the Slater Integrals ... ---> Initial values are taken from M.W.Haverkort's PhD Thesis (p.156) --> Assumed initial configuration: 2p6d8 --> INITIAL STATE PARAMETERS F0dd F2dd F4dd zeta_3d 0.5666 11.0097 6.8373 0.0830 --> Assumed final configuration: 2p5d9 --> FINAL STATE PARAMETERS F0dd F2dd F4dd zeta_3d zeta_2p F2pd G1pd G3pd 0.6025 11.7045 7.2756 0.1020 11.5070 6.9480 5.2047 2.9610 --> Calculating the lowest 45 eigenstates... --> Ground state properties <E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g> -2.706 1.999 12.000 15.154 -0.889 -0.266 -0.334 -1.020 -0.878 2.011 5.989 -2.705 1.999 12.000 15.146 -0.000 -0.004 -0.332 -1.020 -0.878 2.011 5.989 -2.703 1.999 12.000 15.138 0.889 0.257 -0.330 -1.020 -0.878 2.011 5.989 -1.640 1.988 11.988 16.790 -0.167 -0.152 -0.873 -1.019 -0.877 3.008 4.992 -1.640 1.988 11.988 16.795 -0.012 0.001 -0.875 -1.019 -0.877 3.008 4.992 -1.621 1.999 12.000 15.825 -0.442 -0.029 -0.484 -1.020 -0.878 3.007 4.993 -1.621 1.999 12.000 15.835 0.157 0.103 -0.487 -1.020 -0.878 3.007 4.993 -1.620 1.999 12.000 15.840 0.441 0.078 -0.488 -1.020 -0.878 3.008 4.992 -1.570 1.997 11.989 12.550 -0.436 -0.134 0.265 -1.020 -0.877 2.996 5.004 -1.569 1.997 11.989 12.553 -0.058 0.005 0.265 -1.020 -0.877 2.996 5.004 -1.568 1.997 11.989 12.557 0.450 0.122 0.264 -1.020 -0.877 2.996 5.004 -1.549 2.000 12.000 12.001 0.068 -0.014 0.500 -1.020 -0.878 3.000 5.000 -0.944 1.995 11.483 18.926 -0.035 -0.036 -1.474 -1.003 -0.887 3.584 4.416 -0.876 1.999 11.421 15.293 -0.448 0.776 -0.506 -1.002 -0.887 3.568 4.432 -0.876 1.999 11.421 15.303 0.035 0.014 -0.509 -1.002 -0.887 3.569 4.431 -0.876 1.999 11.422 15.309 0.419 -0.769 -0.510 -1.002 -0.887 3.569 4.431 -0.797 1.726 10.766 9.049 -0.012 0.023 -0.081 -0.981 -0.878 3.334 4.666 -0.797 1.726 10.766 9.050 0.011 0.010 -0.081 -0.981 -0.878 3.334 4.666 -0.766 1.997 11.279 9.961 -0.427 0.434 0.788 -0.998 -0.890 3.544 4.456 -0.766 1.997 11.280 9.957 0.006 0.001 0.789 -0.998 -0.890 3.544 4.456 -0.766 1.997 11.280 9.952 0.450 -0.423 0.790 -0.998 -0.890 3.544 4.456 -0.489 0.290 9.837 9.162 0.000 -0.004 1.144 -0.902 -0.808 2.295 5.705 -0.489 0.290 9.837 9.162 0.000 -0.001 1.144 -0.902 -0.808 2.295 5.705 0.459 0.151 7.374 7.664 -0.032 -0.490 -0.716 -0.887 -0.805 3.132 4.868 0.460 0.150 7.379 7.668 -0.000 0.003 -0.715 -0.887 -0.805 3.132 4.868 0.460 0.150 7.384 7.672 0.032 0.489 -0.714 -0.887 -0.805 3.132 4.868 0.804 0.030 18.827 18.853 -0.000 -0.016 0.042 -0.767 -0.843 2.420 5.580 0.923 1.992 2.783 6.359 -0.098 -0.081 -0.304 -0.737 -1.034 3.446 4.554 0.923 1.992 2.782 6.358 -0.008 0.005 -0.306 -0.737 -1.034 3.446 4.554 0.953 1.853 3.252 6.569 -0.417 -0.343 0.404 -0.749 -1.017 3.429 4.571 0.953 1.853 3.250 6.569 0.085 0.078 0.402 -0.749 -1.017 3.429 4.571 0.954 1.853 3.250 6.569 0.414 0.364 0.402 -0.749 -1.017 3.428 4.572 0.987 1.994 2.636 2.910 -0.437 -0.386 0.409 -0.732 -1.037 3.421 4.579 0.988 1.994 2.636 2.909 -0.020 0.017 0.409 -0.732 -1.037 3.420 4.580 0.989 1.994 2.636 2.909 0.454 0.372 0.409 -0.732 -1.037 3.420 4.580 1.019 1.972 2.755 1.287 0.028 -0.024 0.736 -0.731 -1.036 3.402 4.598 1.264 0.009 19.943 19.958 -0.002 -0.448 0.084 -0.776 -0.855 3.003 4.997 1.264 0.009 19.943 19.958 0.000 0.008 0.084 -0.776 -0.855 3.003 4.997 1.265 0.009 19.943 19.958 0.002 0.444 0.085 -0.776 -0.855 3.003 4.997 2.030 0.004 16.629 16.635 -0.000 -0.060 0.119 -0.810 -0.836 3.917 4.083 2.030 0.004 16.628 16.635 0.000 0.010 0.119 -0.810 -0.836 3.917 4.083 2.104 0.004 18.097 18.103 0.000 -1.807 0.090 -0.795 -0.845 3.888 4.112 2.105 0.004 18.101 18.107 0.000 0.054 0.090 -0.795 -0.845 3.888 4.112 2.106 0.004 18.106 18.112 -0.000 1.820 0.090 -0.795 -0.845 3.888 4.112 5.913 0.003 0.936 0.933 0.000 0.000 0.196 -0.581 -0.585 3.594 4.406 Now the finite temperature properties will be calculated. Boltzmann averaging of the M=2Ms+Ml operator and of the X-ray absorption spectra. Partition function is sufficiently converged after Npsi= 2 Z,dZ 1.0000000364703 1.3291678830223e-15 For a magnetic field of ( 5.000000 0.000000 10.000000 ) Tesla At temperature T=1.000000 Kelvin, the magnetic moment is: Spin Orbital Total x 0.44461 0.13279 1.02202 y 0.00000 0.00000 0.00000 z 0.88920 0.26553 2.04393 Printing the components of the conductivity tensor (sigma[i,j]) Printing the XAS spectra Prepare gnuplot-file for XAS spectra Prepare gnuplot-file for Sigma Execute the gnuplot to produce plots and convert the output into a pdf-file FINISHED
For completeness, the actual code is:
- XAS.Quanty
-- script contributed by Yaroslav Kvashnin -- Minimize the output of the program, i.e. for longer calculations -- the program tells the user what it is doing. For these short -- examples the result is instant. Verbosity(0) print("--> This program is the spectra calculator.") print("--> Assuming a specific ionic configuration for Me^{2+} , the L-edge spectra are produced and plotted in a separate file.") print("") print("--> Chosen parameters are as follows:") dofile("conf.in") io.write(" Ion beta 10Dq Bext(x) Bext(y) Bext(z) Temperature","\n") io.write(string.format(" %s %2.7f %2.7f %2.7f %2.7f %2.7f %2.2f ",ion,beta,tenDq,Bx,By,Bz,T)) io.write("\n") print("") print("---> Setting up the Slater Integrals ...") print("---> Initial values are taken from M.W.Haverkort's PhD Thesis (p.156)") print("") if ion=="Cu" then Nelec=9 -- initial state parameters zeta_3d=0.102; F2dd=12.854; F4dd=7.980 -- final state parameters zeta_2p=13.498; F2pd=8.177; G1pd=6.169; G3pd=3.510 -- final state parameters Xzeta_3d=0.124; XF2dd=13.611; XF4dd=8.457 elseif ion=="Ni" then Nelec=8 zeta_3d=0.083; F2dd=12.233; F4dd=7.597 zeta_2p=11.507; F2pd=7.720; G1pd=5.783; G3pd=3.290 Xzeta_3d=0.102; XF2dd=13.005; XF4dd=8.084 elseif ion=="Co" then Nelec=7 zeta_3d=0.066; F2dd=11.604; F4dd=7.209 zeta_2p=9.748; F2pd=7.259; G1pd=5.394; G3pd=3.068 Xzeta_3d=0.083; XF2dd=12.395; XF4dd=7.707 elseif ion=="Fe" then Nelec=6 zeta_3d=0.052; F2dd=10.965; F4dd=6.815 zeta_2p=8.200; F2pd=6.792; G1pd=5.000; G3pd=2.843 Xzeta_3d=0.067; XF2dd=11.778; XF4dd=7.327 elseif ion=="Mn" then Nelec=5 zeta_3d=0.040; F2dd=10.315 ; F4dd=6.413 zeta_2p=6.846; F2pd=6.320 ; G1pd=4.603; G3pd=2.617 Xzeta_3d=0.053; XF2dd=11.154 ; XF4dd=6.942 elseif ion=="Cr" then Nelec=4 zeta_3d=0.030; F2dd=9.648; F4dd=6.001 zeta_2p=5.668; F2pd=5.840; G1pd=4.201; G3pd=2.387 Xzeta_3d=0.041; XF2dd=10.521; XF4dd=6.551 elseif ion=="V" then Nelec=3 zeta_3d=0.022; F2dd=8.961; F4dd=5.576 zeta_2p=4.650; F2pd=5.351; G1pd=3.792; G3pd=2.154 Xzeta_3d=0.031; XF2dd=9.875; XF4dd=6.152 elseif ion=="Ti" then Nelec=2 zeta_3d=0.016; F2dd=8.243; F4dd=5.132 zeta_2p=3.776; F2pd=4.849; G1pd=3.376; G3pd=1.917 Xzeta_3d=0.023; XF2dd=9.21; XF4dd=5.744 elseif ion=="Sc" then Nelec=1 zeta_3d=0.010; F2dd=0; F4dd=0 zeta_2p=3.032; F2pd=4.332; G1pd=2.950; G3pd=1.674 Xzeta_3d=0.017; XF2dd=8.530; XF4dd=5.321 else print("Could not recognize the ion name...") os.exit() end -- scaling with beta factor F2dd=beta*F2dd; F4dd=beta*F4dd F2pd=beta*F2pd; G1pd=beta*G1pd; G3pd=beta*G3pd XF2dd=beta*XF2dd; XF4dd=beta*XF4dd -- number of possible many-body states in the initial configuration Npsi = fact(10) / (fact(Nelec) * fact(10-Nelec)) -- Bringing everything to the same units (eV) T = T * EnergyUnits.Kelvin.value Bx = Bx * EnergyUnits.Tesla.value By = By * EnergyUnits.Tesla.value Bz = Bz * EnergyUnits.Tesla.value -- 10 d-electrons + 6 p-electrons NFermion=16 NBoson=0 -- p-shell [dn] IndexDn_2p={0,2,4} -- p-shell [up] IndexUp_2p={1,3,5} -- d-shell [dn] IndexDn_3d={6,8,10,12,14} -- d-shell [up] IndexUp_3d={7,9,11,13,15} -- define the operators OppSx =NewOperator("Sx" ,NFermion, IndexUp_3d, IndexDn_3d) OppSy =NewOperator("Sy" ,NFermion, IndexUp_3d, IndexDn_3d) OppSz =NewOperator("Sz" ,NFermion, IndexUp_3d, IndexDn_3d) OppSsqr =NewOperator("Ssqr" ,NFermion, IndexUp_3d, IndexDn_3d) OppSplus=NewOperator("Splus",NFermion, IndexUp_3d, IndexDn_3d) OppSmin =NewOperator("Smin" ,NFermion, IndexUp_3d, IndexDn_3d) OppLx =NewOperator("Lx" ,NFermion, IndexUp_3d, IndexDn_3d) OppLy =NewOperator("Ly" ,NFermion, IndexUp_3d, IndexDn_3d) OppLz =NewOperator("Lz" ,NFermion, IndexUp_3d, IndexDn_3d) OppLsqr =NewOperator("Lsqr" ,NFermion, IndexUp_3d, IndexDn_3d) OppLplus=NewOperator("Lplus",NFermion, IndexUp_3d, IndexDn_3d) OppLmin =NewOperator("Lmin" ,NFermion, IndexUp_3d, IndexDn_3d) OppJx =NewOperator("Jx" ,NFermion, IndexUp_3d, IndexDn_3d) OppJy =NewOperator("Jy" ,NFermion, IndexUp_3d, IndexDn_3d) OppJz =NewOperator("Jz" ,NFermion, IndexUp_3d, IndexDn_3d) OppJsqr =NewOperator("Jsqr" ,NFermion, IndexUp_3d, IndexDn_3d) OppJplus=NewOperator("Jplus",NFermion, IndexUp_3d, IndexDn_3d) OppJmin =NewOperator("Jmin" ,NFermion, IndexUp_3d, IndexDn_3d) Oppldots=NewOperator("ldots",NFermion, IndexUp_3d, IndexDn_3d) -- define the coulomb operator -- we here define the part depending on F0 seperately from the part depending on F2 -- when summing we can put in the numerical values of the slater integrals OppF0 =NewOperator("U", NFermion, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2 =NewOperator("U", NFermion, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4 =NewOperator("U", NFermion, IndexUp_3d, IndexDn_3d, {0,0,1}) -- Crystal field operator for the d-shell Akm = PotentialExpandedOnClm("Oh", 2, {0.6,-0.4}) OpptenDq = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh",2,{1,0}); OppNeg = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh",2,{0,1}); OppNt2g = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, Akm) -- Spin-orbit coupling in 2p-shell Oppcldots= NewOperator("ldots", NFermion, IndexUp_2p, IndexDn_2p) -- core hole potentials: -- direct OppUpdF0 = NewOperator("U", NFermion, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {1,0}, {0,0}) OppUpdF2 = NewOperator("U", NFermion, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,1}, {0,0}) -- exchange OppUpdG1 = NewOperator("U", NFermion, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {1,0}) OppUpdG3 = NewOperator("U", NFermion, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {0,1}) t=math.sqrt(1/2); -- setting up the transition operators with various polarisations -- Dipole X Akm = {{1,-1,t},{1, 1,-t}} ; TXASx = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- Dipole Y Akm = {{1,-1,t*I},{1, 1,t*I}} ; TXASy = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- Dipole Z Akm = {{1,0,1}} ; TXASz = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) TXASxpy = t*(TXASx + TXASy) TXASypz = t*(TXASy + TXASz) TXASzpx = t*(TXASz + TXASx) TXASxpiy = t*(TXASx + I * TXASy) TXASypiz = t*(TXASy + I * TXASz) TXASzpix = t*(TXASz + I * TXASx) --- right circular polarisation TXASr = t*(TXASx - I * TXASy) --- left circular polarisation TXASl =-t*(TXASx + I * TXASy) ------------------------------------------------ ----- Input parameters for the Hamiltonian ----- -- in crystal field theory U drops out of the equation U = 0.000 F0dd = U+(F2dd+F4dd)*2/63 XF0dd = U+(XF2dd+XF4dd)*2/63 -- in crystal field theory U drops out of the equation Upd = 0.000 F0pd = Upd + G1pd*1/15 + G3pd*3/70 print("") io.write(string.format("--> Assumed initial configuration: 2p6d%i", Nelec)) llist = {F0dd, F2dd, F4dd, zeta_3d} print("") print("--> INITIAL STATE PARAMETERS") io.write(" F0dd F2dd F4dd zeta_3d\n") for i=1,4 do io.write(string.format("%7.4f ",llist[i])) end print("") print("") io.write(string.format("--> Assumed final configuration: 2p5d%i",Nelec+1)) llist2 = {XF0dd, XF2dd, XF4dd, Xzeta_3d, zeta_2p, F2pd, G1pd, G3pd} print("") print("--> FINAL STATE PARAMETERS") io.write(" F0dd F2dd F4dd zeta_3d zeta_2p F2pd G1pd G3pd \n") for i=1,8 do io.write(string.format("%7.4f ",llist2[i])) end print("") -- initial state Hamiltonian Hamiltonian = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + tenDq*OpptenDq + zeta_3d*Oppldots Hamiltonian = Hamiltonian + Bx * (2*OppSx + OppLx) + By * (2*OppSy + OppLy) + Bz * (2*OppSz + OppLz) -- final state Hamiltonian XASHamiltonian = XF0dd*OppF0 + XF2dd*OppF2 + XF4dd*OppF4 + tenDq*OpptenDq + Xzeta_3d*Oppldots + zeta_2p * Oppcldots + F2pd * OppUpdF2 + G1pd * OppUpdG1 + G3pd * OppUpdG3 XASHamiltonian = XASHamiltonian + Bx * (2*OppSx + OppLx) + By * (2*OppSy + OppLy) + Bz * (2*OppSz + OppLz) -- in order to make sure we have a filling of 2 electrons we need to define some restrictions StartRestrictions = {NFermion, NBoson, {"111111 0000000000",6,6}, {"000000 1111111111",Nelec,Nelec}} print("") print("--> Calculating the lowest", Npsi ,"eigenstates...") psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi) oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSz, OppLz, Oppldots, OppF2, OppF4, OppNeg, OppNt2g}; print("") print("--> Ground state properties") print("") -- Energy of the lowest multiplet. To be shifted to 0 to get a proper partition function Egrd=psiList[1] * Hamiltonian * psiList[1] print(" <E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g>"); for key,value in pairs(psiList) do expvalue = value * oppList * value for k,v in pairs(expvalue) do io.write(string.format("%6.3f ",Complex.Re(v))) end io.write("\n") end print("") print("Now the finite temperature properties will be calculated.") print("Boltzmann averaging of the M=2Ms+Ml operator and of the X-ray absorption spectra.") print("") Z=0 Mx =0 MSx=0 MLx=0 My =0 MSy=0 MLy=0 Mz =0 MSz=0 MLz=0 Spectra_z=0 Spectra_r=0 Spectra_l=0 --- Conductivity tensor Sigma_X=0 Sigma_Y=0 Sigma_Z=0 Sigma_X_p_Y=0 Sigma_Y_p_Z=0 Sigma_Z_p_X=0 Sigma_X_p_IY=0 Sigma_Y_p_IZ=0 Sigma_Z_p_IX=0 Z = 0 ; for j=1, Npsi do dZ = math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) if (dZ < 0.000000001) then print("Partition function is sufficiently converged after Npsi=",j-1) print("Z,dZ",Z,dZ) break end Z = Z + dZ Mx = Mx - psiList[j] * (2 * OppSx + OppLx) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) MSx = MSx - psiList[j] * (OppSx) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) MLx = MLx - psiList[j] * (OppLx) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) My = My - psiList[j] * (2 * OppSy + OppLy) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) MSy = MSy - psiList[j] * (OppSy) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) MLy = MLy - psiList[j] * (OppLy) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Mz = Mz - psiList[j] * (2 * OppSz + OppLz) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) MSz = MSz - psiList[j] * (OppSz) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) MLz = MLz - psiList[j] * (OppLz) * psiList[j] * math.exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Spectra_z = Spectra_z + CreateSpectra(XASHamiltonian, TXASz, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Spectra_r = Spectra_r + CreateSpectra(XASHamiltonian, TXASr, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Spectra_l = Spectra_l + CreateSpectra(XASHamiltonian, TXASl, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_X = Sigma_X + CreateSpectra(XASHamiltonian, TXASx, psiList[j],{{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_Y = Sigma_Y + CreateSpectra(XASHamiltonian, TXASy, psiList[j],{{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_Z = Sigma_Z + CreateSpectra(XASHamiltonian, TXASz, psiList[j],{{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_X_p_Y = Sigma_X_p_Y + CreateSpectra(XASHamiltonian, TXASxpy, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_Y_p_Z = Sigma_Y_p_Z + CreateSpectra(XASHamiltonian, TXASypz, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_Z_p_X = Sigma_Z_p_X + CreateSpectra(XASHamiltonian, TXASzpx, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_X_p_IY = Sigma_X_p_IY + CreateSpectra(XASHamiltonian, TXASxpiy, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_Y_p_IZ = Sigma_Y_p_IZ + CreateSpectra(XASHamiltonian, TXASypiz, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) Sigma_Z_p_IX = Sigma_Z_p_IX + CreateSpectra(XASHamiltonian, TXASzpix, psiList[j], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) * exp(-(psiList[j] * Hamiltonian * psiList[j] - Egrd)/T) end; Mx = Mx / Z MSx = MSx / Z MLx = MLx / Z My = My / Z MSy = MSy / Z MLy = MLy / Z Mz = Mz / Z MSz = MSz / Z MLz = MLz / Z Spectra_z = Spectra_z/Z Spectra_r = Spectra_r/Z Spectra_l = Spectra_l/Z Sigma_X = Sigma_X/Z Sigma_Y = Sigma_Y/Z Sigma_Z = Sigma_Z/Z Sigma_X_p_Y = Sigma_X_p_Y/Z Sigma_Y_p_Z = Sigma_Y_p_Z/Z Sigma_Z_p_X = Sigma_Z_p_X/Z Sigma_X_p_IY = Sigma_X_p_IY/Z Sigma_Y_p_IZ = Sigma_Y_p_IZ/Z Sigma_Z_p_IX = Sigma_Z_p_IX/Z print("") io.write(string.format("For a magnetic field of ( %f %f %f ) Tesla\n", Bx/EnergyUnits.Tesla.value, By/EnergyUnits.Tesla.value, Bz/EnergyUnits.Tesla.value)) io.write(string.format("At temperature T=%f Kelvin, the magnetic moment is:\n", T/EnergyUnits.Kelvin.value)) print(" Spin Orbital Total") io.write(string.format("x %9.5f %9.5f %9.5f\n", Complex.Re(MSx),Complex.Re(MLx),Complex.Re(Mx))) io.write(string.format("y %9.5f %9.5f %9.5f\n", Complex.Re(MSy),Complex.Re(MLy),Complex.Re(My))) io.write(string.format("z %9.5f %9.5f %9.5f\n", Complex.Re(MSz),Complex.Re(MLz),Complex.Re(Mz))) Spectra_ave = (Spectra_z + Spectra_l + Spectra_r)/3 Spectra_XMCD = (Spectra_r - Spectra_l) Sigma_11 = Sigma_X Sigma_22 = Sigma_Y Sigma_33 = Sigma_Z Sigma_12 = Sigma_X_p_Y - I * Sigma_X_p_IY - 0.5 * (1 - I) * (Sigma_X + Sigma_Y) Sigma_21 = Sigma_X_p_Y + I * Sigma_X_p_IY - 0.5 * (1 + I) * (Sigma_Y + Sigma_X) Sigma_13 = Sigma_Z_p_X + I * Sigma_Z_p_IX - 0.5 * (1 + I) * (Sigma_X + Sigma_Z) Sigma_31 = Sigma_Z_p_X - I * Sigma_Z_p_IX - 0.5 * (1 - I) * (Sigma_Z + Sigma_X) Sigma_23 = Sigma_Y_p_Z - I * Sigma_Y_p_IZ - 0.5 * (1 - I) * (Sigma_Y + Sigma_Z) Sigma_32 = Sigma_Y_p_Z + I * Sigma_Y_p_IZ - 0.5 * (1 + I) * (Sigma_Z + Sigma_Y) print("Printing the components of the conductivity tensor (sigma[i,j])") Sigma_11.Print({{"file","Sigma11.dat"}}) Sigma_22.Print({{"file","Sigma22.dat"}}) Sigma_33.Print({{"file","Sigma33.dat"}}) Sigma_12.Print({{"file","Sigma12.dat"}}) Sigma_21.Print({{"file","Sigma21.dat"}}) Sigma_13.Print({{"file","Sigma13.dat"}}) Sigma_31.Print({{"file","Sigma31.dat"}}) Sigma_23.Print({{"file","Sigma23.dat"}}) Sigma_32.Print({{"file","Sigma32.dat"}}) print("Printing the XAS spectra") Spectra_z.Print({{"file","XASSpecZ.dat"}}) Spectra_r.Print({{"file","XASSpecR.dat"}}) Spectra_l.Print({{"file","XASSpecL.dat"}}) Spectra_ave.Print({{"file","XASSpecAVER.dat"}}) Spectra_XMCD.Print({{"file","XASSpecXMCD.dat"}}) -- prepare the gnuplot output for XAS gnuplotInput = [[ set autoscale # scale axes automatically set xtic auto # set xtics automatically set ytic auto # set ytics automatically set style line 1 lt 1 lw 2 lc rgb "#FF0000" set style line 2 lt 1 lw 2 lc rgb "#00FF00" set style line 3 lt 1 lw 2 lc rgb "#0000FF" set style line 4 lt 1 lw 2 lc rgb "#000000" set xlabel "E (eV)" font "Times,12" set ylabel "Intensity (arb. units)" font "Times,12" set out 'XASSpec.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 12 set multiplot layout 4, 1 plot "XASSpecZ.dat" using 1:(-$3) title 'z-polarized' with lines ls 1,\ "XASSpecR.dat" using 1:(-$3) title 'R-polarized' with lines ls 2,\ "XASSpecL.dat" using 1:(-$3) title 'L-polarized' with lines ls 3 plot "XASSpecAVER.dat" using 1:(-$3) title 'Average' with lines ls 4,\ "XASSpecXMCD.dat" using 1:(-$3) title 'XMCD' with lines ls 1 unset multiplot ]] print("Prepare gnuplot-file for XAS spectra") -- write the gnuplot script to a file file = io.open("XASSpec.gnuplot", "w") file:write(gnuplotInput) file:close() -- prepare the gnuplot output for Sigma gnuplotInput = [[ set autoscale # scale axes automatically set xtic auto # set xtics automatically set ytic auto # set ytics automatically set style line 1 lt 1 lw 2 lc 1 set style line 2 lt 1 lw 2 lc 3 set xlabel "E (eV)" font "Times,10" set ylabel "Intensity (arb. units)" font "Times,10" set yrange [-0.3:0.3] set out 'SigmaTensor.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 set multiplot layout 6, 3 plot "Sigma11.dat" u 1:2 title 'Re[{/Symbol s}_{11}]' with lines ls 1,\ "Sigma11.dat" u 1:3 title 'Im[{/Symbol s}_{11}]' with lines ls 2 plot "Sigma12.dat" u 1:2 title 'Re[{/Symbol s}_{12}]' with lines ls 1,\ "Sigma12.dat" u 1:3 title 'Im[{/Symbol s}_{12}]' with lines ls 2 plot "Sigma13.dat" u 1:2 title 'Re[{/Symbol s}_{13}]' with lines ls 1,\ "Sigma13.dat" u 1:3 title 'Im[{/Symbol s}_{13}]' with lines ls 2 plot "Sigma21.dat" u 1:2 title 'Re[{/Symbol s}_{21}]' with lines ls 1,\ "Sigma21.dat" u 1:3 title 'Im[{/Symbol s}_{21}]' with lines ls 2 plot "Sigma22.dat" u 1:2 title 'Re[{/Symbol s}_{22}]' with lines ls 1,\ "Sigma22.dat" u 1:3 title 'Im[{/Symbol s}_{22}]' with lines ls 2 plot "Sigma23.dat" u 1:2 title 'Re[{/Symbol s}_{23}]' with lines ls 1,\ "Sigma23.dat" u 1:3 title 'Im[{/Symbol s}_{23}]' with lines ls 2 plot "Sigma31.dat" u 1:2 title 'Re[{/Symbol s}_{31}]' with lines ls 1,\ "Sigma31.dat" u 1:3 title 'Im[{/Symbol s}_{31}]' with lines ls 2 plot "Sigma32.dat" u 1:2 title 'Re[{/Symbol s}_{32}]' with lines ls 1,\ "Sigma32.dat" u 1:3 title 'Im[{/Symbol s}_{32}]' with lines ls 2 plot "Sigma33.dat" u 1:2 title 'Re[{/Symbol s}_{33}]' with lines ls 1,\ "Sigma33.dat" u 1:3 title 'Im[{/Symbol s}_{33}]' with lines ls 2 unset multiplot ]] print("Prepare gnuplot-file for Sigma") -- write the gnuplot script to a file file = io.open("SigmaTensor.gnuplot", "w") file:write(gnuplotInput) file:close() print("") print("Execute the gnuplot to produce plots and convert the output into a pdf-file") -- call gnuplot to execute the script os.execute("gnuplot XASSpec.gnuplot ; ps2pdf XASSpec.ps ; ps2eps XASSpec.ps ; mv XASSpec.eps temp.eps ; eps2eps temp.eps XASSpec.eps ; rm temp.eps") os.execute("gnuplot SigmaTensor.gnuplot ; ps2pdf SigmaTensor.ps ; ps2eps SigmaTensor.ps ; mv SigmaTensor.eps temp.eps ; eps2eps temp.eps SigmaTensor.eps ; rm temp.eps") print("FINISHED")