Energy level diagram

Example four shows the calculation of an energy level diagram of Ni$^{2+}$ as a function of the cubic crystal field parameter. Temperature leads to an occupation of excited states according to Bolzman statistics. It then becomes important to know the excited states. Here we calculate a graph showing these states as a function of the crystal-filed parameters. Although crystal field theory is often a highly oversimplified theory not accurate enough to describe a system well, degeneracies are given by symmetry and the here obtained energy level diagram will mostly change quantitative, but not qualitative when going to more involved methods of calculating material properties.

The text output written to screen does not show much interesting information.

Energy_Level_Diagram.out

--> In this example we shall plot the energy-level diagram (so-called 'Tanabe-Sugano Diagram')
--> Energy levels will be printed a function of 10Dq parameter, representing the crystal field strength
--> Setting up the d-shell
--> d8 (2 holes)  configuration has 45 possible states
 
 
--> Initial Hamiltonian: H_e-e + H_SO + H_Zeeman
--> H0 = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + zeta_3d*Oppldots + Bz*(2*OppSz + OppLz);
 
=================================
--> List of parameters:
--> F2dd    = 11.142
--> F4dd    =  6.874
--> F0dd    = U+(F2dd+F4dd)*2/63
--> zeta_3d = 0.081
--> Bz      = 0.000001
=================================
 
--> Diagonalising...
 
--> Adding the Crystal field as a perturbation: H' = H0 + x * H_CF
--> start increasing x ...
10Dq = 0.000 0.010 0.020 0.030 0.040 0.050 0.060 0.070 0.080 0.090 0.100 0.110 0.120 0.130 0.140 0.150 0.160 0.170 0.180 0.190 0.200 0.210 0.220 0.230 0.240 0.250 0.260 0.270 0.280 0.290 0.300 0.310 0.320 0.330 0.340 0.350 0.360 0.370 0.380 0.390 0.400 0.410 0.420 0.430 0.440 0.450 0.460 0.470 0.480 0.490 0.500 0.510 0.520 0.530 0.540 0.550 0.560 0.570 0.580 0.590 0.600 0.610 0.620 0.630 0.640 0.650 0.660 0.670 0.680 0.690 0.700 0.710 0.720 0.730 0.740 0.750 0.760 0.770 0.780 0.790 0.800 0.810 0.820 0.830 0.840 0.850 0.860 0.870 0.880 0.890 0.900 0.910 0.920 0.930 0.940 0.950 0.960 0.970 0.980 0.990 1.000 1.010 1.020 1.030 1.040 1.050 1.060 1.070 1.080 1.090 1.100 1.110 1.120 1.130 1.140 1.150 1.160 1.170 1.180 1.190 1.200 1.210 1.220 1.230 1.240 1.250 1.260 1.270 1.280 1.290 1.300 1.310 1.320 1.330 1.340 1.350 1.360 1.370 1.380 1.390 1.400 1.410 1.420 1.430 1.440 1.450 1.460 1.470 1.480 1.490 1.500 1.510 1.520 1.530 1.540 1.550 1.560 1.570 1.580 1.590 1.600 1.610 1.620 1.630 1.640 1.650 1.660 1.670 1.680 1.690 1.700 1.710 1.720 1.730 1.740 1.750 1.760 1.770 1.780 1.790 1.800 1.810 1.820 1.830 1.840 1.850 1.860 1.870 1.880 1.890 1.900 1.910 1.920 1.930 1.940 1.950 1.960 1.970 1.980 1.990 2.000 2.010 2.020 2.030 2.040 2.050 2.060 2.070 2.080 2.090 2.100 2.110 2.120 2.130 2.140 2.150 2.160 2.170 2.180 2.190 2.200 2.210 2.220 2.230 2.240 2.250 2.260 2.270 2.280 2.290 2.300 2.310 2.320 2.330 2.340 2.350 2.360 2.370 2.380 2.390 2.400 2.410 2.420 2.430 2.440 2.450 2.460 2.470 2.480 2.490 2.500 2.510 2.520 2.530 2.540 2.550 2.560 2.570 2.580 2.590 2.600 2.610 2.620 2.630 2.640 2.650 2.660 2.670 2.680 2.690 2.700 2.710 2.720 2.730 2.740 2.750 2.760 2.770 2.780 2.790 2.800 2.810 2.820 2.830 2.840 2.850 2.860 2.870 2.880 2.890 2.900 2.910 2.920 2.930 2.940 2.950 2.960 2.970 2.980 2.990 3.000 

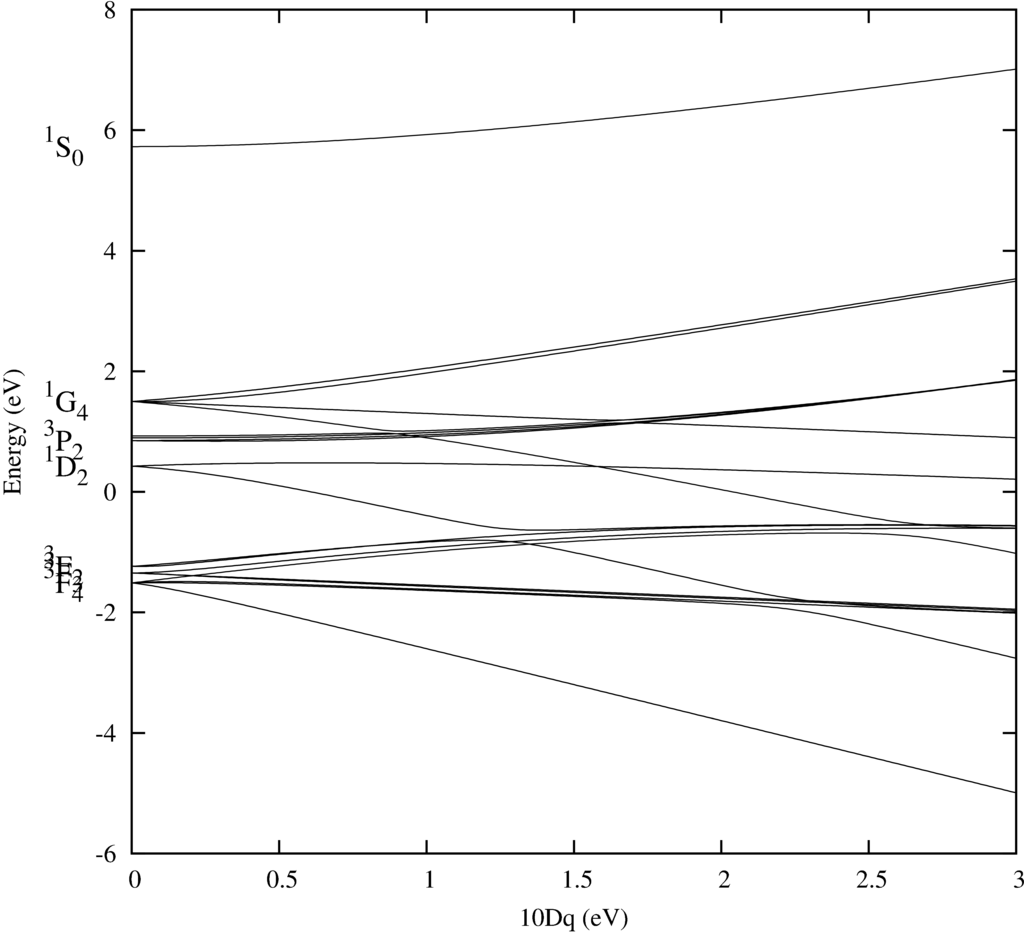
The energy level diagram of Ni$^{2+}$. i.e. the energy of the 45 eigen-states of 8 electrons in a $d$-shell as a function of the crystal-field splitting.

But the pdf created (see above) shows the energy level diagram. For $10Dq=0$ one has spherical symmetry and retrieves the atomic energy levels. We plotted the term symbols next to the level energies. Increasing the crystal field leads to a splitting of these levels and at some point to a mixing.

For completeness, the actual code is:

Energy_Level_Diagram.Quanty

-- Minimize the output of the program, i.e. for longer calculations
-- the program tells the user what it is doing. For these short
-- examples the result is instant.
Verbosity(0)
 
print("--> In this example we shall plot the energy-level diagram (so-called 'Tanabe-Sugano Diagram')") 
print("--> Energy levels will be printed a function of 10Dq parameter, representing the crystal field strength") 
print("--> Setting up the d-shell")
 
-- number of available fermionic spin-orbitals (d-shell in the present case)
NFermion=10;      
-- number of bosonic states (phonons, etc...)                
NBoson=0;     
-- indices for the "spin-dn" states                    
IndexDn_3d={0,2,4,6,8};  
-- indices for the "spin-up" states         
IndexUp_3d={1,3,5,7,9};           
 
-- function to print Term symbols
function LSJ2term (S2,L2,J2)
  L = math.floor(0.5 * (math.sqrt(math.abs(L2) * 4 +1) - 1) + 0.5)
  if     L == 0   then str1="S"
  elseif L == 1   then str1="P"
  elseif L == 2   then str1="D"
  elseif L == 3   then str1="F"
  elseif L == 4   then str1="G"
  elseif L == 5   then str1="H"
  elseif L == 6   then str1="I"
  elseif L == 7   then str1="K"
  elseif L == 8   then str1="L"
  elseif L == 9   then str1="M"
  elseif L == 10  then str1="N"
  elseif L == 11  then str1="O"
  elseif L == 12  then str1="Q"
  elseif L == 13  then str1="R"
  elseif L == 14  then str1="T"
  elseif L == 15  then str1="U"
  elseif L == 16  then str1="V"
  elseif L == 17  then str1="W"
  elseif L == 18  then str1="X"
  elseif L == 19  then str1="Y"
  elseif L == 20  then str1="Z"
  else 
    str1="?"
  end
  mult = math.floor(math.sqrt(S2 * 4 +1)+0.5)
  twoJ = math.floor((math.sqrt(math.abs(J2) * 4 +1) - 1) + 0.5)
  if( 2*math.floor((twoJ+0.5)/2)==twoJ ) then
    return "^{"..mult.."}"..str1.."_{"..(twoJ/2).."}"
  else
    return "^{"..mult.."}"..str1.."_{"..twoJ.."/2}"
  end  
end
 
-- Here we define the operators in the space of chosen orbitals
 
OppSx   =NewOperator("Sx"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppSy   =NewOperator("Sy"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppSz   =NewOperator("Sz"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppSsqr =NewOperator("Ssqr" ,NFermion, IndexUp_3d, IndexDn_3d)
OppSplus=NewOperator("Splus",NFermion, IndexUp_3d, IndexDn_3d)
OppSmin =NewOperator("Smin" ,NFermion, IndexUp_3d, IndexDn_3d)
 
OppLx   =NewOperator("Lx"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppLy   =NewOperator("Ly"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppLz   =NewOperator("Lz"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppLsqr =NewOperator("Lsqr" ,NFermion, IndexUp_3d, IndexDn_3d)
OppLplus=NewOperator("Lplus",NFermion, IndexUp_3d, IndexDn_3d)
OppLmin =NewOperator("Lmin" ,NFermion, IndexUp_3d, IndexDn_3d)
 
OppJx   =NewOperator("Jx"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppJy   =NewOperator("Jy"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppJz   =NewOperator("Jz"   ,NFermion, IndexUp_3d, IndexDn_3d)
OppJsqr =NewOperator("Jsqr" ,NFermion, IndexUp_3d, IndexDn_3d)
OppJplus=NewOperator("Jplus",NFermion, IndexUp_3d, IndexDn_3d)
OppJmin =NewOperator("Jmin" ,NFermion, IndexUp_3d, IndexDn_3d)
 
-- Spin-orbit coupling
Oppldots=NewOperator("ldots",NFermion, IndexUp_3d, IndexDn_3d)
 
-- e-e Coulomb repulsion
OppF0 =NewOperator("U", NFermion, IndexUp_3d, IndexDn_3d, {1,0,0})
OppF2 =NewOperator("U", NFermion, IndexUp_3d, IndexDn_3d, {0,1,0})
OppF4 =NewOperator("U", NFermion, IndexUp_3d, IndexDn_3d, {0,0,1})
 
-- Expansion of the effective electron-ion potential in the certain symmetry ("Oh" group in this case)
-- This operator splits the states: it lowers one manifold on 0.4 [e.u.] and lifts the other on 0.6 [e.u.]
-- in the limit of very strong CF we can call these manifolds as T2g and Eg
Akm = PotentialExpandedOnClm("Oh", 2, {0.6,-0.4})
OpptenDq = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, Akm)
 
-- We can define the operator which will count the number of particles in each manifold
Akm = PotentialExpandedOnClm("Oh", 2, {1,0})
OppNeg = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, Akm)
Akm = PotentialExpandedOnClm("Oh", 2, {0,1})
OppNt2g = NewOperator("CF", NFermion, IndexUp_3d, IndexDn_3d, Akm)
 
print("--> d8 (2 holes)  configuration has 45 possible states")
print("")
-- Here we set up the parameters for the operators, defined above.
Npsi=45;
U       =  0.000
F2dd    = 11.142 
F4dd    =  6.874
F0dd    = U+(F2dd+F4dd)*2/63
zeta_3d = 0.081
Bz      = 0.000001
 
print("")
print("--> Initial Hamiltonian: H_e-e + H_SO + H_Zeeman")
print("--> H0 = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + zeta_3d*Oppldots + Bz*(2*OppSz + OppLz);")
print("")
print("=================================")
print("--> List of parameters:");
print("--> F2dd    = 11.142")
print("--> F4dd    =  6.874")
print("--> F0dd    = U+(F2dd+F4dd)*2/63")
print("--> zeta_3d = 0.081")
print("--> Bz      = 0.000001")
print("=================================")
print("")
 
-- Setting up the initial Hamiltonian in the 2nd quantised form
-- Note: here we do not have the CF
Hamiltonian0 =  F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + zeta_3d*Oppldots + Bz*(2*OppSz + OppLz);
-- We shall now diagonalise the Hamiltonian, looking for the states with the specific occupation (8 in this case).
StartRestrictions = {NFermion, NBoson,  {"1111111111",8,8}}
 
print("--> Diagonalising...")
-- Diagonalisation of the initial Hamiltonian (no CF)
psiList = Eigensystem(Hamiltonian0, StartRestrictions, Npsi)
 
TermSymbol={} ; TermSymbol[0]=""; E0={} ;E0[0]=0
for i =1,Npsi do
  S2=psiList[i] * OppSsqr * psiList[i]
  L2=psiList[i] * OppLsqr * psiList[i]
  J2=psiList[i] * OppJsqr * psiList[i]
  E0[i]=psiList[i] * Hamiltonian0 * psiList[i]
  TermSymbol[i]=LSJ2term(S2,L2,J2)
end
 
-- Open up the file, where the data will be stored
file = assert(io.open("EnergyLevelDiagram", "w"))
 
print("")
print("--> Adding the Crystal field as a perturbation: H' = H0 + x * H_CF")
print("--> start increasing x ...")
io.write("10Dq = ")
-- We add the CF to the Hamiltonian and start varying its strength. Each time we update the H, we re-diagonalise it.
for i=0, 300 do
  tenDq = 0.01*i
  file:write(string.format("%14.7E ",tenDq))
  io.write(string.format("%5.3f ",tenDq))
  io.flush()
  Hamiltonian=Hamiltonian0 + tenDq * OpptenDq
  Eigensystem(Hamiltonian, psiList)
  for key,value in pairs(psiList) do
    energy = value * Hamiltonian * value
    file:write(string.format("%14.7E ",energy))
  end
  file:write("\n")
end
file:close()
io.write("\n")
 
-- The output will be supplied to the gnuplot for consequent visualisation
-- Starting the preparation of the gnuplot-input file
 
gnuplotInput = [[
set terminal postscript portrait enhanced color  "Times" 12
set autoscale                          # scale axes automatically
set xtic auto                          # set xtics automatically
set ytic auto                          # set ytics automatically
set style line  1 lt 1 lw 1 lc rgb "#000000"
 
set xlabel "10Dq (eV)" font "Times,12"
set ylabel "Energy (eV)" font "Times,12" offset -3
 
set out 'EnergyLevelDiagram.ps'
set size 1.0, 0.625
]]
 
-- write the gnuplot script to a file
file = io.open("EnergyLevelDiagram.gnuplot", "w")
file:write(gnuplotInput)
 
for i=1,Npsi do
  if (abs(E0[i]-E0[i-1]) > 0.1 and TermSymbol[i] ~= TermSymbol[i-1]) then
  	file:write("set label \""..TermSymbol[i].."\" at  -0.3,",E0[i]," font \"Times,14\"\n")
  end 
end
 
gnuplotInput=[[
plot for [i=2:46] "EnergyLevelDiagram" using 1:i notitle with lines ls  1
]]
 
file:write(gnuplotInput)
file:close()
 
-- call gnuplot to execute the script
os.execute("gnuplot EnergyLevelDiagram.gnuplot ; ps2pdf EnergyLevelDiagram.ps ; ps2eps EnergyLevelDiagram.ps ; mv EnergyLevelDiagram.eps temp.eps ; eps2eps temp.eps EnergyLevelDiagram.eps ; rm temp.eps")