Energy level diagram
In order to do temperature averaging it is important to understand the number of excited states that are important. One can learn a lot by looking at the energy level diagram. Here we plot one for Ni$^{2+}$.
The input file is:
- Energy_level_diagram.Quanty
-- For NiO we know that 10Dq=1.1 eV, however if you have a new compound you might roughly -- know these values, but never exactly. It is then nice to see how the eigen-state -- energies change as a function of 10Dq. -- plots were one shows the eigen-state energy as a function of some parameter (crystal- -- field strength) are called energy level diagrams or Sugano - Tanabe diagrams -- here we create the diagram for Ni - d8 -- in order to minimize the output of the calculation we set the verbosity to 0 Verbosity(0) -- we have a single d-shell in the bases and thus need 10 Fermions, grouped in 5 orbitals -- with spin down and 5 with spin up. NF=10 NB=0 IndexDn_3d={0,2,4,6,8} IndexUp_3d={1,3,5,7,9} -- again we define several operators OppSx =NewOperator("Sx" ,NF, IndexUp_3d, IndexDn_3d) OppSy =NewOperator("Sy" ,NF, IndexUp_3d, IndexDn_3d) OppSz =NewOperator("Sz" ,NF, IndexUp_3d, IndexDn_3d) OppSsqr =NewOperator("Ssqr" ,NF, IndexUp_3d, IndexDn_3d) OppSplus=NewOperator("Splus",NF, IndexUp_3d, IndexDn_3d) OppSmin =NewOperator("Smin" ,NF, IndexUp_3d, IndexDn_3d) OppLx =NewOperator("Lx" ,NF, IndexUp_3d, IndexDn_3d) OppLy =NewOperator("Ly" ,NF, IndexUp_3d, IndexDn_3d) OppLz =NewOperator("Lz" ,NF, IndexUp_3d, IndexDn_3d) OppLsqr =NewOperator("Lsqr" ,NF, IndexUp_3d, IndexDn_3d) OppLplus=NewOperator("Lplus",NF, IndexUp_3d, IndexDn_3d) OppLmin =NewOperator("Lmin" ,NF, IndexUp_3d, IndexDn_3d) OppJx =NewOperator("Jx" ,NF, IndexUp_3d, IndexDn_3d) OppJy =NewOperator("Jy" ,NF, IndexUp_3d, IndexDn_3d) OppJz =NewOperator("Jz" ,NF, IndexUp_3d, IndexDn_3d) OppJsqr =NewOperator("Jsqr" ,NF, IndexUp_3d, IndexDn_3d) OppJplus=NewOperator("Jplus",NF, IndexUp_3d, IndexDn_3d) OppJmin =NewOperator("Jmin" ,NF, IndexUp_3d, IndexDn_3d) Oppldots=NewOperator("ldots",NF, IndexUp_3d, IndexDn_3d) OppF0 =NewOperator("U",NF, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2 =NewOperator("U",NF, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4 =NewOperator("U",NF, IndexUp_3d, IndexDn_3d, {0,0,1}) Akm = PotentialExpandedOnClm("Oh",2,{0.6,-0.4}) OpptenDq = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh",2,{1,0}) OppNeg = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh",2,{0,1}) OppNt2g = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- for d^8 there are 10*9/2 = 45 different states. For a diagram we want to calculate all Npsi=45 -- as before we can set the parameters, in this case all but 10Dq U = 0.000 F2dd = 11.142 F4dd = 6.874 F0dd = U+(F2dd+F4dd)*2/63 zeta_3d = 0.081 Bz = 0.000001 -- and we define the Hamiltonian as a sum of prefactors times operators. Note that -- we do not include the crystal field here. Hamiltonian0 = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + zeta_3d*Oppldots + Bz*(2*OppSz + OppLz) -- We first calculate the eigen states of Hamiltonian0. For a filling of 8 electrons -- the wavefunctions are stored as a table in the variable psiList StartRestrictions = {NF, NB, {"1111111111",8,8}} psiList = Eigensystem(Hamiltonian0, StartRestrictions, Npsi) -- We will write the eigen energies to the file EnergyLevelDiagram, which we open for writing -- The variable file now points to the file "EnergyLevelDiagram" file = assert(io.open("EnergyLevelDiagram", "w")) -- no we need to loop over the value of 10Dq and for each value diagonalize the Hamiltonian -- and save the eigenvalues to the file EnergyLevelDiagram -- we do 301 calculations changing 10Dq from 0 to 3 in steps of 10 meV. -- i is an index that counts from 0 to 300 -- tenDq is a variable equal to 0.01*i and the actual crystal-field strength. -- During the loop we write the value of 10Dq to the screen so we know where the calculation is -- Into the file we write first the value of 10Dq and then the 45 eigenvalues -- but in order to calculate the eigenvalues we first need to call the function Eigensystem -- acting on Hamiltonian0 + tenDq * OpptenDq -- Eigensystem is a flexible function that can be used in different ways and on different -- objects. If you have a set of states close to the eigenstates you are interested in you can -- use these states as starting point. -- Calling Eigensystem with an operator as the first argument and a table of functions as the second -- will change the functions to become the lowest eigenstates of the operator. io.write("10Dq = ") for i=0, 300 do tenDq = 0.01*i io.write(string.format("%5.3f ",tenDq)) io.flush() file:write(string.format("%14.7E ",tenDq)) Hamiltonian=Hamiltonian0 + tenDq * OpptenDq Eigensystem(Hamiltonian, psiList) for key,value in pairs(psiList) do energy = value * Hamiltonian * value file:write(string.format("%14.7E ",energy)) end file:write("\n") end io.write("\n") file:close() -- Once we have created a file containing the eigenenergies we can make a plot -- A gnuplot script that would make this plot can be found below gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set xlabel "10Dq (eV)" font "Times,12" set ylabel "Energy (eV)" font "Times,12" set out 'EnergyLevelDiagram.ps' set size 1.0, 0.625 set terminal postscript portrait enhanced color "Times" 12 plot for [i=2:46] "EnergyLevelDiagram" using 1:i notitle with lines ls 1 ]] -- write the gnuplot script to a file file = io.open("EnergyLevelDiagram.gnuplot", "w") file:write(gnuplotInput) file:close() -- call gnuplot to execute the script os.execute("gnuplot EnergyLevelDiagram.gnuplot") -- change the postscript file to pdf or eps os.execute("ps2pdf EnergyLevelDiagram.ps ; ps2eps EnergyLevelDiagram.ps ; mv EnergyLevelDiagram.eps temp.eps ; eps2eps temp.eps EnergyLevelDiagram.eps ; rm temp.eps")
As in the example in the beginning of the tutorial Quanty returns a nice plot. Note that one can add labeling. For this have a look at the example in the beginning of the tutorial.
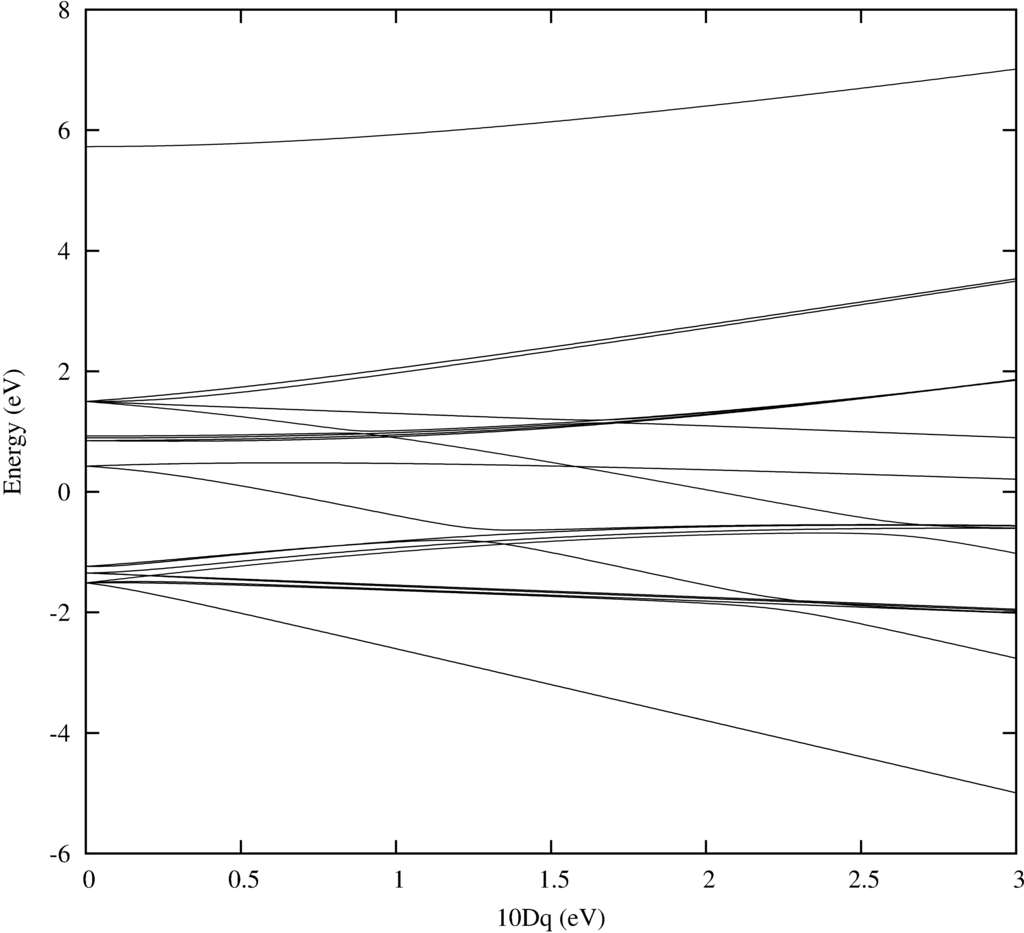
The text output is trivial and just shows counters that tell you in which loop you are during the calculation:
- Energy_level_diagram.out
10Dq = 0.000 0.010 0.020 0.030 0.040 0.050 0.060 0.070 0.080 0.090 0.100 0.110 0.120 0.130 0.140 0.150 0.160 0.170 0.180 0.190 0.200 0.210 0.220 0.230 0.240 0.250 0.260 0.270 0.280 0.290 0.300 0.310 0.320 0.330 0.340 0.350 0.360 0.370 0.380 0.390 0.400 0.410 0.420 0.430 0.440 0.450 0.460 0.470 0.480 0.490 0.500 0.510 0.520 0.530 0.540 0.550 0.560 0.570 0.580 0.590 0.600 0.610 0.620 0.630 0.640 0.650 0.660 0.670 0.680 0.690 0.700 0.710 0.720 0.730 0.740 0.750 0.760 0.770 0.780 0.790 0.800 0.810 0.820 0.830 0.840 0.850 0.860 0.870 0.880 0.890 0.900 0.910 0.920 0.930 0.940 0.950 0.960 0.970 0.980 0.990 1.000 1.010 1.020 1.030 1.040 1.050 1.060 1.070 1.080 1.090 1.100 1.110 1.120 1.130 1.140 1.150 1.160 1.170 1.180 1.190 1.200 1.210 1.220 1.230 1.240 1.250 1.260 1.270 1.280 1.290 1.300 1.310 1.320 1.330 1.340 1.350 1.360 1.370 1.380 1.390 1.400 1.410 1.420 1.430 1.440 1.450 1.460 1.470 1.480 1.490 1.500 1.510 1.520 1.530 1.540 1.550 1.560 1.570 1.580 1.590 1.600 1.610 1.620 1.630 1.640 1.650 1.660 1.670 1.680 1.690 1.700 1.710 1.720 1.730 1.740 1.750 1.760 1.770 1.780 1.790 1.800 1.810 1.820 1.830 1.840 1.850 1.860 1.870 1.880 1.890 1.900 1.910 1.920 1.930 1.940 1.950 1.960 1.970 1.980 1.990 2.000 2.010 2.020 2.030 2.040 2.050 2.060 2.070 2.080 2.090 2.100 2.110 2.120 2.130 2.140 2.150 2.160 2.170 2.180 2.190 2.200 2.210 2.220 2.230 2.240 2.250 2.260 2.270 2.280 2.290 2.300 2.310 2.320 2.330 2.340 2.350 2.360 2.370 2.380 2.390 2.400 2.410 2.420 2.430 2.440 2.450 2.460 2.470 2.480 2.490 2.500 2.510 2.520 2.530 2.540 2.550 2.560 2.570 2.580 2.590 2.600 2.610 2.620 2.630 2.640 2.650 2.660 2.670 2.680 2.690 2.700 2.710 2.720 2.730 2.740 2.750 2.760 2.770 2.780 2.790 2.800 2.810 2.820 2.830 2.840 2.850 2.860 2.870 2.880 2.890 2.900 2.910 2.920 2.930 2.940 2.950 2.960 2.970 2.980 2.990 3.000